*다익스트라 알고리즘(Dijkstra Algorithm)
-> 다익스트라 알고리즘은 음의 가중치(음의 간선, 음의 값)가 없는 그래프의 한 노드에서 각 모든 노드까지의 최단거리를 구하는 알고리즘을 말한다.
-> 초기 모델은 O(V^2)의 시간복잡도를 가졌다. 이후 우선순위 큐 등을 이용한 고안된 알고리즘이 탄생했고, 현재는 O((V+E)log V)의 시간복잡도를 가지고 있다(만일 연결 그래프라면 O(ElogV)까지 시간 복잡도를 줄일 수 있다고 한다). 일반적으로는 그래프가 희소 그래프인 경우에 우선순위 큐를 이용하는 것이 낫다고 한다.
※음의 가중치를 가지면 안되는 이유는 최소 비용의 음의 무한대 발산, 그리디 알고리즘 적용 불가능 등이 있다. 후자는 제일 아래에 있는 다익스트라 알고리즘 정당성 증명을 참고하도로 하자.
※연결 그래프 : 모든 두 꼭짓점 사이에 경로가 존재하는 그래프.
※희소 그래프 : 밀집 그래프의 반대. 밀집 그래프란, 간선의 수가 최대에 가까운 그래프를 만한다. 보통, 간선의 총 개수가 정점의 개수^2과 근사하다면 밀집 그래프이다.
*다익스트라 알고리즘의 매커니즘
-> 다익스트라 알고리즘은 기본적으로 그리디 알고리즘이자 다이나믹 프로그래밍 기법을 사용한 알고리즘이다.
-> 다익스트라 알고리즘은 기본적으로 아래 두 단계를 반복하여 임의의 노드에서 각 모든 노드까지의 최단거리를 구한다. 임의의 노드에서 다른 노드로 가는 값을 비용이라고 한다.
(1) 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택한다(그리디 알고리즘).
(2) 해당 노드로부터 갈 수 있는 노드들의 비용을 갱신한다(다이나믹 프로그래밍).
-> 예를 들어 아래 그림에서, A노드에서 출발하여 F노드로 가는 최단 경로를 구하는 문제를 다익스트라 알고리즘을 적용하여 생각해보자.

각 단계마다 기준이 필요하기 때문에, 지금부터는 방문하지 않은 노드의 집합을 Before, 방문한 노드의 집합을 After, 현재까지 A노드가 방문한 곳 까지의 최소 비용을 D[대상 노드]라고 정의하도록 하자. 그렇다면 현재 각 집합이 가지고 있는 값은 다음과 같은 것 이다.

<초기화 단계>
그렇다면, 이 상태에서 방문하지 않은 노드 중 가장 비용이 적은 대상 노드는 어디일까? A노드에서 다른 간선으로 가는 비용이 0인 간선이 존재하지 않는다면, 당연히 A노드일 것이다. 또한, 그러한 값이 존재한다고 하더라도 첫 번째 단계에서는 'A노드에서 A노드로 가는 지점이 가장 짧다'라고 그냥 정의하고 시작한다. 즉, 첫 번째 단계에서는 가장 비용이 적은 노드를 선택할 기준이 없기 때문에 출발지인 A노드 자신을 초기 선택 노드로 초기화한다.

<알고리즘 적용>
초기화가 끝났으니, 이제 앞서 언급한 두 가지 논리를 그냥 반복해서 적용하면 끝이다. 위 상태에서 방문하지 않은 노드 중 가장 비용이 적은 대상 노드는 어디 인가? 당연히 A노드이다. 또한, A노드를 기준으로 갈 수 있는 인접 노드로의 최소 비용은 얼마일까? 결과는 아래와 같을 것이다.

다음 단계는 어떨까? 앞선 단계를 그냥 계속 반복하기만 하면 된다. 현재 상태에서 방문하지 않은 노드 중 가장 비용이 적은 노드는 어디 인가? A노드는 방문 하였기 때문에 B노드가 될 것이다. 따라서 B노드를 방문하고, B노드와 인접한 노드들의 최소 비용을 갱신해주면 된다.

다음 단계도 마찬가지이다. 이제는 A노드와 B노드를 방문하였기 때문에, 그 중에서 가장 비용이 적은 노드인 D를 선택하고 방문한 뒤 같은 과정을 진행해주면 된다. 이후 과정은 생략하고 그림과 그림 설명으로 대체하도록 하겠다.
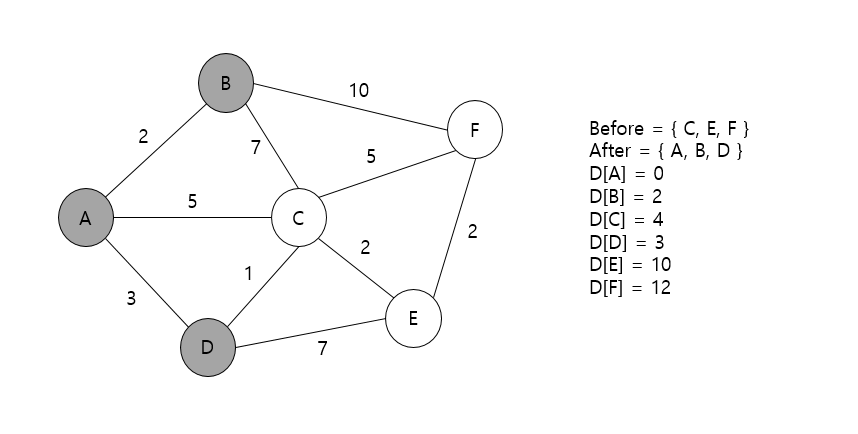
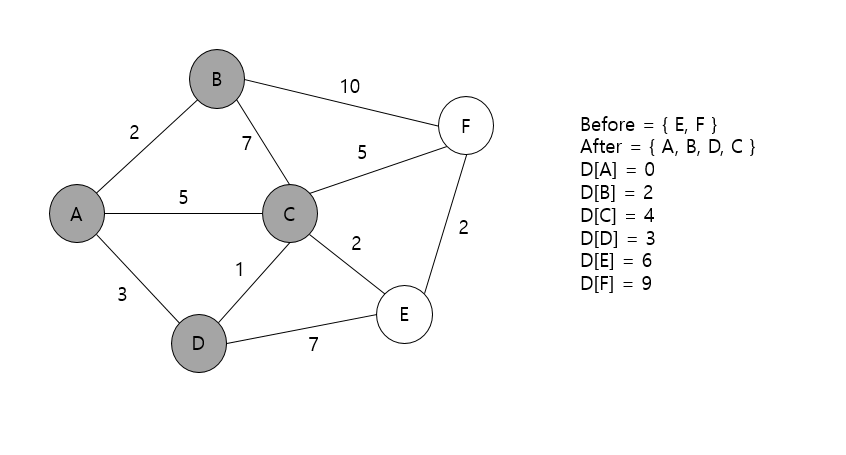
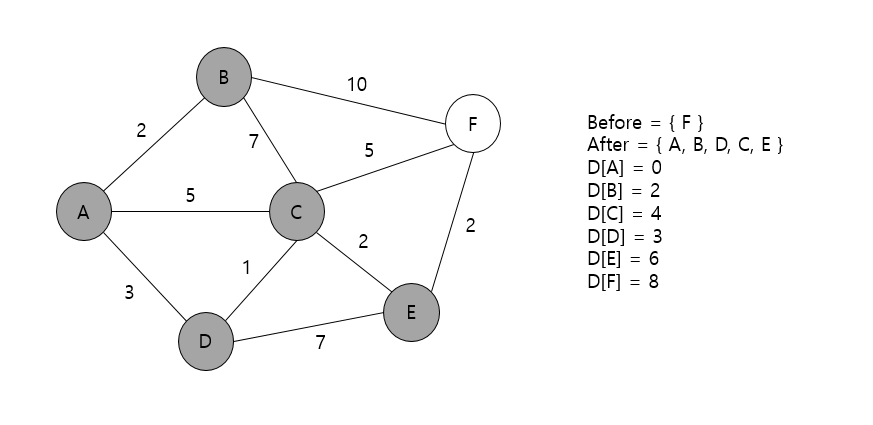
마지막으로 방문해야하는 노드인 F에서는 더 이상 갈 수 있는 노드가 존재하지 않으므로, 방문만 완료하고 알고리즘을 종료해주면 된다.
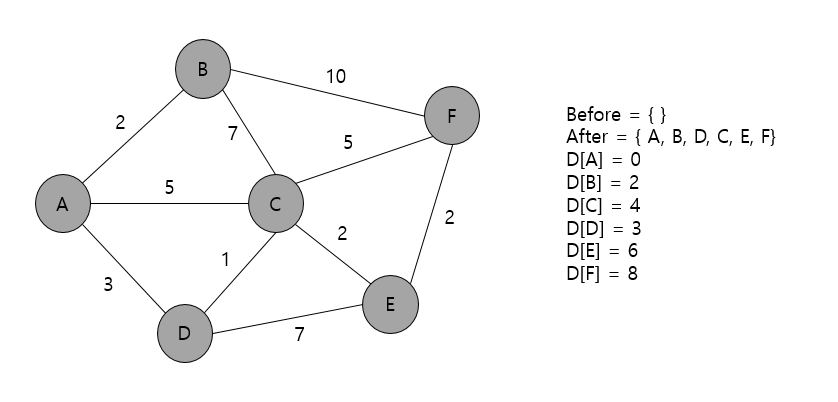
따라서, 다익스트라 알고리즘에 의한 A노드부터 F노드까지(혹은 A노드부터 각 모든 정점 까지)의 최소 비용은 위와 같은 값을 가진다.
*다익스트라 알고리즘의 구현 : O(V^2)
->우선 위의 로직을 구현하기 위해서는 입력으로 주어진 그래프를 저장하는 방법을 알아야 한다. 그래프를 표현하는 방법이 미숙하다면 아래 게시글을 참고하도록 하자.sskl660.tistory.com/60
[Java]그래프의 표현
*그래프의 표현 ->프로그래밍을 하다보면 그래프를 만들어야 하는 경우가 발생할 수 있는데, 프로그래밍에서 그래프를 그리를 방법은 크게 2가지(인접 행렬, 인접 리스트)로 나뉜다. ->인접 행렬
sskl660.tistory.com
->한 번 방문한 배열은 방문할 수 없으므로 방문 여부를 체크할 배열이 필요할 것이고, 각 노드 까지의 최소 비용을 저장할 배열이 필요할 것이다.
->구현에서 고려해 주어야 하는 것은, 미방문 지점의 값을 항상 최소의 값으로 갱신하는 것이 목표이기 때문에, 미 방문 지점은 매우 큰 값으로 초기화하여 로직을 처리해주면 된다(구할 수 있다면, 노드가 가질 수 있는 최대 비용을 넣어두어도 된다).
->최소 비용을 갖는 노드을 선택하는 과정은 앞선 일반적인 구현에서는 최악의 경우 모든 노드을 확인해야 하고, 이 것은 V번 반복하기 때문에 O(V^2)의 시간 복잡도를 갖는다.
package Graph;
import java.util.ArrayList;
import java.util.Scanner;
/*
sample input
5 6
1
5 1 1
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6
*/
// 도착 지점과, 도착지점으로 가는 비용을 의미하는 클래스를 정의한다.
class Node {
int idx;
int cost;
// 생성자
Node(int idx, int cost) {
this.idx = idx;
this.cost = cost;
}
}
public class Dijkstra {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 노드와 간선의 개수
int V = sc.nextInt();
int E = sc.nextInt();
// 출발지점
int start = sc.nextInt();
// 1. 인접리스트를 이용한 그래프 초기화
ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
// 노드의 번호가 1부터 시작하므로, 0번 인덱스 부분을 임의로 만들어 놓기만 한다.
for (int i = 0; i < V + 1; i++) {
graph.add(new ArrayList<>());
}
// 그래프에 값을 넣는다.
for (int i = 0; i < E; i++) {
// a로 부터 b로 가는 값은 cost이다.
int a = sc.nextInt();
int b = sc.nextInt();
int cost = sc.nextInt();
graph.get(a).add(new Node(b, cost));
}
// 2. 방문 여부를 확인할 boolean 배열, start 노드부터 end 노드 까지의 최소 거리를 저장할 배열을 만든다.
boolean[] visited = new boolean[V + 1];
int[] dist = new int[V + 1];
// 3. 최소 거리 정보를 담을 배열을 초기화 한다.
for (int i = 0; i < V + 1; i++) {
// 출발 지점 외 나머지 지점까지의 최소 비용은 최대로 지정해둔다.
dist[i] = Integer.MAX_VALUE;
}
// 출발 지점의 비용은 0으로 시작한다.
dist[start] = 0;
// 4. 다익스트라 알고리즘을 진행한다.
// 모든 노드을 방문하면 종료하기 때문에, 노드의 개수 만큼만 반복을 한다.
for (int i = 0; i < V; i++) {
// 4 - 1. 현재 거리 비용 중 최소인 지점을 선택한다.
// 해당 노드가 가지고 있는 현재 비용.
int nodeValue = Integer.MAX_VALUE;
// 해당 노드의 인덱스(번호).
int nodeIdx = 0;
// 인덱스 0은 생각하지 않기 때문에 0부터 반복을 진행한다.
for (int j = 1; j < V + 1; j++) {
// 해당 노드를 방문하지 않았고, 현재 모든 거리비용 중 최솟값을 찾는다.
if (!visited[j] && dist[j] < nodeValue) {
nodeValue = dist[j];
nodeIdx = j;
}
}
// 최종 선택된 노드를 방문처리 한다.
visited[nodeIdx] = true;
// 4 - 2. 해당 지점을 기준으로 인접 노드의 최소 거리 값을 갱신한다.
for (int j = 0; j < graph.get(nodeIdx).size(); j++) {
// 인접 노드를 선택한다.
Node adjNode = graph.get(nodeIdx).get(j);
// 인접 노드가 현재 가지는 최소 비용과
// 현재 선택된 노드의 값 + 현재 노드에서 인접 노드로 가는 값을 비교하여 더 작은 값으로 갱신한다.
if (dist[adjNode.idx] > dist[nodeIdx] + adjNode.cost) {
dist[adjNode.idx] = dist[nodeIdx] + adjNode.cost;
}
}
}
// 5. 최종 비용을 출력한다.
for (int i = 1; i < V + 1; i++) {
if (dist[i] == Integer.MAX_VALUE) {
System.out.println("INF");
} else {
System.out.println(dist[i]);
}
}
sc.close();
}
}
*다익스트라 알고리즘의 구현(우선순위 큐 이용) : O((V+E)log V)
->기본적으로 다익스트라 알고리즘은 최소 비용을 갖는 노드를 선택하고, 주변 노드의 값을 갱신하였다. 그렇다면, 비용을 나타내는 배열에서 갱신된 노드를 제외하고는 여전히 INF의 값을 갖기 때문에 굳이 고려해줄 필요가 없음을 알게 된다. 즉, 갱신하는 주변 노드의 값에 대해서만 다음 최소 비용을 갖는 노드를 선택해주면 된다는 것이 우선순위큐를 이용하는 것의 핵심이다.
->우선 순위큐에 들어가는 노드의 수 = 갱신해야하는 주변 노드의 수라고 하였다. 이 말을 다르게하면, 갱신해야하는 주변 노드의 수 = 갱신해야 하는 주변 노드로의 간선의 수를 말한다. 즉, 우선 순위 큐에 삽입하는 최대 횟수는 간선의 개수이다. 따라서, 모든 간선에 대하여 삽입 연산이 발생하기 때문에 최대 O(ElogE)의 시간이 걸릴 것이다. 그런데, 희소 그래프의 경우 E <= V^2이므로, 최대 O(ElogV)의 시간이 걸린다고도 볼 수 있다. 각 노드들을 우선순위큐에 추출해주는 연산에대해서는 최대 V개의 노드에 대하여 우선순위큐에서 추출할 것이므로 최대 O(VlogV)의 시간이 걸릴 것이고 따라서 최대 모든 노드, 간선에대하여 우선 순위큐를 계산해줘야 하므로 O((V+E)logV)의 시간이 걸릴 것 이다.
※주의할 점
->우선 순위큐에 넣는 다음 노드는 최소 비용으로 선택된 노드의 주변 노드라고 하였다. 그런데, 이 주변 노드를 무차별적으로 우선순위큐에 넣고 무차별적으로 검사를 한다면 문제가 발생한다. 즉, 최소 비용으로 뽑은 노드의 방문 체크를 하지 않는 경우와 갱신이 이루어 지지 않는 노드까지 우선 순위큐에 넣는 경우 모두 중복된 노드를 재 방문 하게 되는 문제가 발생한다. 자세한 내용은 아래 코드의 주석을 참고하자.
->시간 복잡도의 핵심은 poll() 연산(최소 비용을 뽑는 연산)과 offer() 연산(최소 비용 후보를 우선 순위큐에 넣는 연산)이다. 만일, 중복 노드를 무차별적으로 큐에 넣는다면 위에서 결과적으로 말한 최대 V개의 노드에서 우선순위큐를 추출하는 O(VlogV)가 보장되지 못한다. 따라서, 중복 노드 방문을 두 가지 조건을 기반으로 방지한다.
package Graph;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
/*
sample input
5 6
1
5 1 1
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6
*/
public class Dijkstra2 {
static int V, E, start;
static ArrayList<ArrayList<Node>> graph;
static class Node {// 다음 노드의 인덱스와, 그 노드로 가는데 필요한 비용을 담고 있다.
int idx, cost;
Node(int idx, int cost) {
this.idx = idx;
this.cost = cost;
}
}
public static void main(String[] args) throws IOException {
// 초기화
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
start = Integer.parseInt(br.readLine());
graph = new ArrayList<ArrayList<Node>>();
for (int i = 0; i < V + 1; i++) {
graph.add(new ArrayList<Node>());
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
// 문제에서는 유향 그래프에서의 다익스트라 알고리즘(이 조건도 문제에 따라 중요하다!).
graph.get(s).add(new Node(e, c));
}
// 다익스트라 알고리즘 초기화
int[] dist = new int[V + 1]; // 최소 비용을 저장할 배열
for (int i = 0; i < V + 1; i++) {
dist[i] = Integer.MAX_VALUE;
}
// 주의점 1. 다익스트라 알고리즘의 최소비용을 기준으로 추출해야 한다. 최대 비용을 기준으로 하는 경우 최악의 경우 지수시간 만큼의 연산을
// 해야한다!
PriorityQueue<Node> q = new PriorityQueue<Node>((o1, o2) -> Integer.compare(o1.cost, o2.cost));
// 시작 노드에서, 시작 노드로 가는 값이 초기에 가장 짧은 비용을 갖는 노드이다.
// 즉, 도착 정점은 start, 비용은 0인 노드를 가장 먼저 선택할 것이다.
q.offer(new Node(start, 0));
// 해당 노드를 선택한 것이나 마찬가지 이므로, dist[start] = 0으로 갱신.
dist[start] = 0;
while (!q.isEmpty()) {
Node curNode = q.poll();
// 목표 정점이 꺼내 졌다면, 해당 노드까지는 최솟값 갱신이 완료 되었다는 것이 확정이다(다익스트라 알고리즘).
// 따라서, 반복문을 종료해도 되지만, 해당 코드는 시작 정점에 대하여 모든 정점으로의 최단 경로를 구하는 것을 가정한다.
// 아래 주석된 코드는 목표 정점이 구해졌다면 빠르게 탈출할 수 있는 조건이다.
// if (curNode.idx == end) {
// System.out.println(dist[curNode.idx]);
// return;
// }
// 꺼낸 노드 = 현재 최소 비용을 갖는 노드.
// 즉, 해당 노드의 비용이 현재 dist배열에 기록된 내용보다 크다면 고려할 필요가 없으므로 스킵한다.
// 주의점 2 : 중복노드 방지1 : 만일, 이 코드를 생략한다면, 언급한 내용대로 이미 방문한 정점을 '중복하여 방문'하게 된다.
// 만일 그렇다면, 큐에 있는 모든 다음 노드에대하여 인접노드에 대한 탐색을 다시 진행하게 된다.
// 그래프 입력이 만일 완전 그래프의 형태로 주어진다면, 이 조건을 생략한 것 만으로 시간 복잡도가 E^2에 수렴할 가능성이 생긴다.
if (dist[curNode.idx] < curNode.cost) {
continue;
}
// 선택된 노드의 모든 주변 노드를 고려한다.
for (int i = 0; i < graph.get(curNode.idx).size(); i++) {
Node nxtNode = graph.get(curNode.idx).get(i);
// 만일, 주변 노드까지의 현재 dist값(비용)과 현재 선택된 노드로부터 주변 노드로 가는 비용을 비교하고, 더 작은 값을 선택한다.
// 주의점 3 : 중복노드 방지 2 : 만일, 조건문 없이 조건문의 내용을 수행한다면 역시 중복 노드가 발생한다.
// 간선에 연결된 노드를 모두 넣어준다면 앞서 언급한 정점의 시간 복잡도 VlogV를 보장할 수 없다.
// 마찬가지로 E^2에 수렴할 가능성이 생긴다. 따라서 이 조건 안에서 로직을 진행해야만 한다.
if (dist[nxtNode.idx] > curNode.cost + nxtNode.cost) {
dist[nxtNode.idx] = curNode.cost + nxtNode.cost;
// 갱신된 경우에만 큐에 넣는다.
q.offer(new Node(nxtNode.idx, dist[nxtNode.idx]));
}
}
}
// 결과 출력
System.out.println(Arrays.toString(dist));
}
}'Study > 개발일지' 카테고리의 다른 글
| [백엔드TIL] 싱글톤패턴 구현 방법 학습 (0) | 2023.11.15 |
|---|---|
| [백엔드TIL] SET, TreeSet, LinkedHashSet 개념 (1) | 2023.11.13 |
| [백엔드TIL] JAVA 조이스틱의 상,하 조작으로 원하는 알파벳 조작하기 (1) | 2023.11.09 |
| [백엔드TIL] 그리디 알고리즘(탐욕법, Greedy Algorithm) (0) | 2023.11.08 |
| [백엔드TIL] 트랜잭션의 고립 수준 (0) | 2023.11.02 |