💡 그리디 알고리즘(탐욕법, Greedy Algorithm) 이란?
- 최적의 값을 구해야 하는 상황에서 사용되는 근시안적인 방법론으로 ‘각 단계에서 최적이라고 생각되는 것을 선택’ 해 나가는 방식으로 진행하여 최종적인 해답에 도달하는 알고리즘입니다.
- 이때, 항상 최적의 값을 보장하는것이 아니라 최적의 값의 ‘근사한 값’을 목표로 하고 있습니다.
- 주로 문제를 분할 가능한 문제들로 분할한 뒤, 각 문제들에 대한 최적해를 구한 뒤 이를 결합하여 전체 문제의 최적해를 구하는 경우에 주로 사용됩니다.
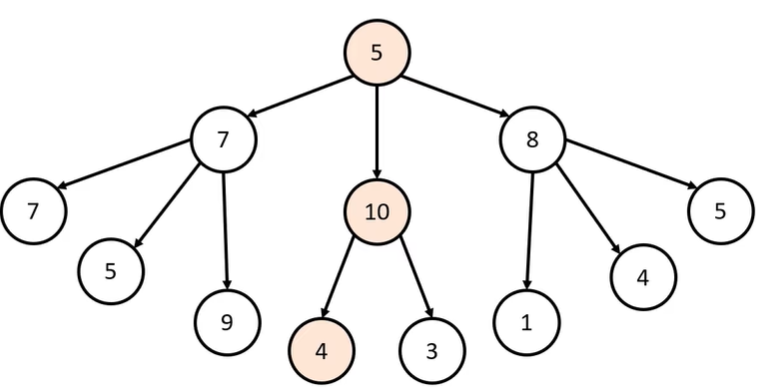
💡 [문제] 노드에서 가장 합이 높은 방법을 선택하는 방법을 생각해 봅니다.
💡 해당 경우에서는 기준 없이 선택을 하는 경우를 보여주고 있습니다.

💡 해당 경우에서는 그리디 알고리즘과 같은 형태로 노드를 선택하는 방식입니다.
💡 각각 상황에서 '최적'이라고 생각하는 방법을 선택합니다.(상황에서 가장 높은 수를 선택합니다.)
[ 더 알아보기 ]
💡 근시안적 방법론이란?
- 단기적인 목표를 중심으로 한 전략적인 접근 방법을 의미합니다. 이 방법론은 주로 현재의 문제를 해결하는 데 초점을 맞추며, 장기적인 전망보다는 단기적인 성과를 중요시합니다.
💡 근사 알고리즘(Approximation Algorithm) 이란?
- 최적의 해를 구할 수 없는 문제에서 근사한 해를 구하는 알고리즘을 의미합니다. 근사 알고리즘은 항상 최적해를 보장하지는 않지만, 많은 경우에는 최적해에 근접한 값을 구할 수 있습니다
2) 그리디 알고리즘 주요 속성
💡 문제를 풀 때 두 가지 조건이 성립해야 그리디 알고리즘을 적용할 수 있습니다.
1. 탐욕 선택 속성(Greedy Choice Property)
💡 탐욕 선택 속성(Greedy Choice Property) 이란?
- 각 단계에서 ‘최선의 선택’을 했을 때 전체 문제에 대한 최적해를 구할 수 있는 경우를 말합니다. 즉, 각 단계에서 가장 이상적인 선택을 하는 것이 전체적으로 최적의 결과를 가져온다는 것입니다.
2. 최적 부분 구조(Optimal Substructure)
💡 최적 부분 구조(Optimal Substructure) 란?
- 전체 문제의 최적해가 ‘부분 문제의 최적해로 구성’될 수 있는 경우를 말합니다. 즉, 전체 문제를 작은 부분 문제로 나누어 각각의 부분 문제에서 최적의 해를 구한 후 이를 조합하여 전체 문제의 최적해를 구하는 것을 의미합니다.
3) 그리디 알고리즘 단계
💡 그리디 알고리즘의 단계는 매 단계마다 최적이라고 생각되는 선택을 하면서 최종적으로 전체적으로 최적인 해답을 찾아내는 과정을 의미합니다.
💡 그리디 알고리즘의 단계
1. 문제의 최적해 구조를 결정합니다.
2. 문제의 구조에 맞게 선택 절차를 정의합니다 : 선택 절차(Selection Procedure)
3. 선택 절차에 따라 선택을 수행합니다.
4. 선택된 해가 문제의 조건을 만족하는지 검사합니다 : 적절성 검사(Feasibility Check)
5. 조건을 만족하지 않으면 해당 해를 제외합니다.
6. 모든 선택이 완료되면 해답을 검사합니다 : 해답 검사(Solution Check)
7. 조건을 만족하지 않으면 해답으로 인정되지 않습니다.
1단계: 선택 절차(Selection Procedure)
💡 선택 절차(Selection Procedure)란?
- 이 단계에서는 ‘현재 상태’에서 ‘최적인 선택’을 합니다. 이 선택은 이후에는 바뀌지 않습니다.
2단계 : 적절성 검사(Feasibility Check)
💡 적절성 검사(Feasibility Check)란?
- 이 단계에서는 선택한 항목이 ‘문제의 조건’을 만족시키는지 확인합니다. 조건을 만족시키지 않으면 해당 항목은 제외됩니다.
3단계: 해답 검사(Solution Check)
💡 해답 검사(Solution Check) 란?
- 이 단계에서는 모든 선택이 완료되면, ‘최종 선택’이 ‘문제의 조건을 만족’시키는지 확인합니다. 조건을 만족시키면 해답으로 인정됩니다.
4) 그리디 알고리즘 vs 동적 계획법
💡 비슷한 방법으로 해결이 되는 동적 계획법과 비교를 해봅니다.
| 분류 | 그리디 알고리즘(Greedy Algorithm) | 동적 계획법(DP: Dynamic Programming) |
| 설명 | 그리디 알고리즘은 각 단계에서 최적의 선택을 하는 방식으로 문제를 해결하는 방식 | 동적 계획법은 작은 문제의 해를 메모이제이션하여 중복 계산을 피하고, 이를 이용하여 큰 문제를 해결하는 방식 |
| 성립 조건 | 1. 탐욕 선택 속성(Greedy Choice Property) 2. 최적 부분 구조(Optimal Substructure) |
1. 중복 부분 문제 (Overlapping Subproblems) 2. 최적 부분 구조 (Optimal Substructure) |
| 중복 부분 문제 | 그리디 알고리즘은 중복 부분 문제를 해결하지 않습니다. | 동적 계획법은 중복 부분 문제를 해결할 수 있습니다. |
| 상황 | 모든 상황을 계산하여 최적의 경로를 구할 수 있습니다 - 모든 상황을 계산하기에 시간이 오래 걸립니다. |
각 단계의 상황에서 최적을 선택하여 최적의 경로를 구합니다. - 최적이 아닌 경우가 될수 있거나 혹은 풀리지 않는 문제가 될수 있습니다. |
출처: https://adjh54.tistory.com/212 [Contributor9:티스토리]
728x90
'Study > 개발일지' 카테고리의 다른 글
| [백엔드TIL]다익스트라 알고리즘(Dijkstra Algorithm) 원리 (0) | 2023.11.10 |
|---|---|
| [백엔드TIL] JAVA 조이스틱의 상,하 조작으로 원하는 알파벳 조작하기 (1) | 2023.11.09 |
| [백엔드TIL] 트랜잭션의 고립 수준 (0) | 2023.11.02 |
| [백엔드TIL] REST API 설계 시 고려사항 (0) | 2023.11.01 |
| [백엔드TIL] JSP와 Servlet 개념 (0) | 2023.10.31 |


